The following post was initially one of my assignments for an independent study in modern physics in my penultimate year as an undergraduate. While studying this problem the text that I used to verify my answer was:
R. Eisberg and R. Resnick, Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles. John Wiley & Sons. 1985. 6.
One of the hallmarks of quantum theory is the Schrödinger equation. There are two forms: the time-dependent and the time-independent equation. The former can be turned into the latter by way of assuming stationary states in which case there is no time evolution (i.e. the time derivative  .
.  denotes the derivative of the wavefunction
denotes the derivative of the wavefunction  with respect to time.)
with respect to time.)
The wavefunction describes the state of a system, and it is found by solving the Schrödinger equation. In this post, I’ll be considering a step potential in which
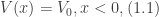
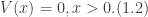
After solving for the wavefunction, I will calculate the reflection and transmission coefficients for the case where the energy of the electron is less than that of the step potential  .
.
First, we assume that we are dealing with stationary states, by doing so we assume that there is no time-dependence. The wavefunction  becomes an eigenfunction (eigen– is German for “characteristic” e.g. characteristic function, characteristic value (eigenvalue), and so on),
becomes an eigenfunction (eigen– is German for “characteristic” e.g. characteristic function, characteristic value (eigenvalue), and so on),  . There are requirements for this eigenfunction in the context of quantum mechanics: eigenfunction
. There are requirements for this eigenfunction in the context of quantum mechanics: eigenfunction  and its first order spatial derivative
and its first order spatial derivative  must be finite, single-valued, and continuous. Using the wavefunction, we write the time-independent Schrödinger equation as
must be finite, single-valued, and continuous. Using the wavefunction, we write the time-independent Schrödinger equation as
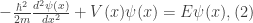
where 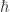 is the reduced Planck’s constant
is the reduced Planck’s constant  , m is the mass of the particle,
, m is the mass of the particle, 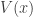 represents the potential, and
represents the potential, and  is the energy.
is the energy.
Now, in electron scattering there are two cases regarding a step potential: the case for which  and the case for which
and the case for which  The focus of this post is the former case. In such a case, the potential is given mathematically by Eqs. (1.1) and (1.2) and can be depicted by the image below:
The focus of this post is the former case. In such a case, the potential is given mathematically by Eqs. (1.1) and (1.2) and can be depicted by the image below:

Image Credit: http://physics.gmu.edu/~dmaria/590%20Web%20Page/public_html/qm_topics/potential/barrier/STUDY-GUIDE.htm
The first part of this problem is to solve for  when
when 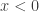 . Then Eq.(2) becomes
. Then Eq.(2) becomes

where 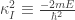 . Eq.(3) is a second order linear homogeneous ordinary differential equation with constant coefficients and can be solved using a characteristic equation. We assume that the solution is of the general form
. Eq.(3) is a second order linear homogeneous ordinary differential equation with constant coefficients and can be solved using a characteristic equation. We assume that the solution is of the general form

which upon taking the first and second order spatial derivatives and substituting into Eq.(3) yields

We can factor out the exponential and recalling that the graph of 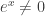 (except in the limit
(except in the limit  )we can then conclude that
)we can then conclude that
 .
.
Hence, 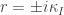 . Therefore, we can write the solution Schrödinger equation in the region
. Therefore, we can write the solution Schrödinger equation in the region 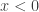 as
as
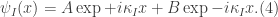
This is the eigenfunction for the first region. Coefficients A and B will be determined later.
Now we can use the same logic for the Schrödinger equation in the region 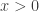 where
where 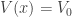 :
:

where ![\kappa_{II}\equiv \frac{\sqrt[]{2m(E-V_{0})}}{\hbar}](https://s0.wp.com/latex.php?latex=%5Ckappa_%7BII%7D%5Cequiv+%5Cfrac%7B%5Csqrt%5B%5D%7B2m%28E-V_%7B0%7D%29%7D%7D%7B%5Chbar%7D&bg=ffffff&fg=333333&s=0&c=20201002) . The general solution for this region is
. The general solution for this region is
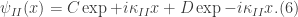
Now the next step is taken using two different approaches: the first using a mathematical argument and the other from a conceptual interpretation of the problem at hand. The former is this: Suppose we let  . What results is that the first term on the right hand side of Eq.(6) diverges (i.e. becomes arbitrarily large). The second term on the right hand side ends up going to zero (it converges). Therefore, D remains finite, hence
. What results is that the first term on the right hand side of Eq.(6) diverges (i.e. becomes arbitrarily large). The second term on the right hand side ends up going to zero (it converges). Therefore, D remains finite, hence 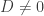 . However, in order to suppress the divergence of the first term, we let
. However, in order to suppress the divergence of the first term, we let 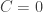 . Thus we arrive at the eigenfunction for
. Thus we arrive at the eigenfunction for 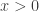
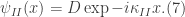
The latter argument is this: In the region 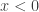 , the first term of the solution represents a wave propagating in the positive x-direction, while the second denotes a wave traveling in the negative x-direction. Similarly, in the region where
, the first term of the solution represents a wave propagating in the positive x-direction, while the second denotes a wave traveling in the negative x-direction. Similarly, in the region where 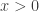 , the first term corresponds to a wave traveling in the positive x-direction. However, this cannot be because the energy of the wave is not sufficient enough to overcome the potential. Therefore, the only term that is relevant here for this region is the second term, for it is a wave propagating in the negative x-direction.
, the first term corresponds to a wave traveling in the positive x-direction. However, this cannot be because the energy of the wave is not sufficient enough to overcome the potential. Therefore, the only term that is relevant here for this region is the second term, for it is a wave propagating in the negative x-direction.
We now determine the coefficients A and B. Recall that the eigenfunction must satisfy the following continuity requirements

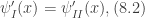
evaluated when 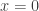 . Doing so in Eqs. (4) and (7), and equating them we arrive at the continuity condition for
. Doing so in Eqs. (4) and (7), and equating them we arrive at the continuity condition for 
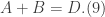
Taking the derivative of 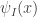 and
and  and evaluating them for when
and evaluating them for when 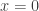 we arrive at
we arrive at

If we add Eqs. (9) and (10) we get the value for the coefficient A in terms of the arbitrary constant D
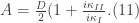
Conversely, if we subtract (9) and (10) we get the value for B in terms of D

Now the reflection coefficient defined as
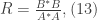
which is the probability that an incident electron (wave) will be reflected. On the other hand, the transmission coefficient is the probability that an electron will be transmitted through the potential (e.g. barrier potential). These two also must satisfy the relation
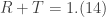
This means that the probability that the electron will be reflected or transmitted is 100%. Therefore, to evaluate R (the reason why I don’t calculate T will become apparent shortly), we take the complex conjugate of A and B and using them in Eq.(13) we get
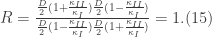
What this conceptually means is that the probability that the electron is reflected is 100%. This implies that it is impossible for an electron to be transmitted through the potential for this system.
. By the method used in a previous section of the aforementioned text, we may write
, and introducing a variational parameter
we have
with respect to
yielding
. Since
for any
, then the terms in the brackets must vanish, yielding the Euler-Lagrange Equation for several dependent variables.






