Astrophysics/Astronomy – Understanding Physics and Astronomy

Basics of Tensor Calculus & General Relativity|A Digression into Special Relativity

So far in this series I have given the definitions of vectors, scalars, tensors, and manifolds. As a result, much of this series has been mostly mathematics and not necessarily physics. To that end, the purpose of this post is to develop the salient points of special relativity. Namely, the intention of this post is to cover the following:

Definition of Inertial Reference Frames: Standard Configuration and Einstein’s Postulates.
Development of the Lorentz Transformation Matrix
Discussion of the Newtonian geometry of spacetime
Discussion of the Minkowski geometry of spacetime (i.e. no curvature)
Finally I will show that the quantity $\delta s^{2}$ is invariant with respect to Lorentz transformations. This is a pretty standard problem in most GR textbooks and in fact in some introductory books on SR.

Continue reading Basics of Tensor Calculus & General Relativity|A Digression into Special Relativity

Astrophysics Series: Derivation of the Total Energy of a Binary Orbit

SOURCE FOR CONTENT: An Introduction to Modern Astrophysics, Carroll & Ostlie, Cambridge University Press. Ch.2 Celestial Mechanics

Here is my solution to one of the problems in the aforementioned text. I derive the total energy of a binary system making use of center-of-mass coordinates. In order to conceptualize it I have used the binary Alpha Centauri A and Alpha Centauri B. While writing this I stumbled upon the Kepler problem, the two-body problem, and the N-body problem. Leave a comment if you would like me to consider that in another post.

Clear Skies!

Derivation of the Total Energy of a Binary Orbit:

Setup: Consider the nearest binary star system to our solar system: Alpha Centauri A and Alpha Centauri B. These two stars orbit each other about a common center of mass; a point called a barycenter. The orbital radius vector of Alpha Centauri A is $\textbf{r}_{1}$ and the orbital radius vector of Alpha Centauri B is $\textbf{r}_{2}$ . The masses of Alpha Centauri A and B are $m_{1}$ , and $m_{2}$ , respectively. The total mass of the binary orbit $M$ is the sum of the individual masses of each component. In the context of this system, we encounter what is called the two-body problem of which there exists a special case known as the Kepler Problem (by the way let me know if that would be something that you guys would want to see…). We can simplify this two-body problem by making use of center-of-mass coordinates wherein we define the reduced mass $\mu$ . Therefore, the derivation of the total energy of the binary system of Alpha Centauri A and B will be carried out in such a coordinate system.

To derive this energy equation, one would typically make use of center-of-mass coordinates in which

$\displaystyle \textbf{r}_{1}=-\frac{\mu}{m_{1}}r, (0.1)$

and

$\displaystyle \textbf{r}_{2}=\frac{\mu}{m_{2}}r, (0.2)$

where $\mu$ represents the reduced mass given by

$\displaystyle \mu\equiv \frac{m_{1}m_{2}}{m_{1}+m_{2}}=\frac{m_{1}m_{2}}{M}. (0.3)$

Recall from conservation of energy that

$\displaystyle E = \frac{1}{2}m_{1}\dot{r}_{1}^{2}+\frac{1}{2}m_{2}\dot{r}_{2}^{2}-G\frac{m_{1}m_{2}}{|\mathcal{R}|}, (1)$

where $|\mathcal{R}|$ represents the separation distance between the two components. Let us take the derivative of Eqs.(0.1) and (0.2) to get

$\displaystyle \dot{r}_{1}=-\frac{\mu}{m_{1}}v, (2.1)$

and

$\displaystyle \dot{r}_{2}= \frac{\mu}{m_{2}}v. (2.2)$

Substitution yields

$\displaystyle E = \frac{1}{2}\frac{\mu^{2}}{m_{1}}v^{2}+\frac{1}{2}\frac{\mu^{2}}{m_{2}}v^{2}-G\frac{m_{1}m_{2}}{|\mathcal{R}|}. (3)$

Upon making use of the definition of the reduced mass (Eq. (0.3)) we arrive at

$\displaystyle E = \frac{1}{2}\mu v^{2}-G\frac{M \mu}{|\mathcal{R}|}. (4)$

If we solve for $m_{1}m_{2}$ in Eq.(0.3) we get the total energy of the binary Alpha Centauri A and B. This is true for any binary system assuming center-of-mass coordinates.

Observing the Variable Star W Ursae Majoris

While I was an undergraduate, one of my smaller research projects involved observing the variable star W Ursae Majoris.

In general, there are six types of binary star systems: Optical double, Visual binary, Astrometric binary, Eclipsing binary, Spectrum binary, and Spectroscopic binary.

In this project, my classmate and I were interested in the eclipsing binary (EW) W Ursae Majoris. An eclipsing binary is a binary system in which one of the stars will pass in front of its companion, effectively causing an eclipse. We are able to observe this by way of generating the light curves of the system. An example light curve is shown below:

(Image was obtained at the URL: https://imagine.gsfc.nasa.gov/educators/hera_college/binary-model.html)

The graph shows a plot of intensity over time (which in this case is an orbital period). Observations of an EW should show dips in the intensity of the two stars. What is really fascinating to me is that we can gain valuable information from this graph. For example, the length of a dip can indicate the masses of the star. If we have a star of mass $m_{1}$ and the other is $m_{2}$ such that $m_{2}>m_{1}$ , and if the duration of the decrease in intensity of the system is significant we can then infer that the mass passing in front of its companion is that of $m_{1}$ . By default, the mass that is being “eclipsed” is $m_{2}$ . Conversely, if the intensity decreases but only for a short while, the positions are reversed, with $m_{2}$ passing in front (relatively speaking) and $m_{1}$ is being “eclipsed”. (I am assuming that the barycenter (i.e. the system’s center of mass) is equidistant from the centers of the two stars.)

Another form of classification of binary stars is whether or not the binary system components are touching or not. More precisely, there are three kinds of close binaries: detached, semi-detached, and contact binary. There are sub-categories of contact binaries: near contact, contact, overcontact, and double contact.

An equipotential surface map of a system (assuming that the binary system has a mass ratio of 2:1, which may be incorrect as most W UMa binaries have a mass ratio of 10:1) is shown below:

Image Credit: Fig.1 of Terrell, D., Eclipsing Binary Stars: Past, Present, and Future. JAAVSO Vol. 30, 2001.

To quickly elaborate, each type of contact binary will fill its inner Lagrangian surface (aka Roche lobes) to an extent. In the context of our project, W Ursae Majoris is an overcontact eclipsing binary system. This type of binary will overfill its inner Lagrangian surface. As a result of this, processes such as mass transfer and accretion can occur. The diagram below shows the orbital evolution of a W UMa EW AC Bootis (in addition to being its own binary system, W UMa is also a class of close binaries)

Image Credit: Fig. 15 of Alton, K., A Unified Roche-Model Light Curve Solution for the W UMa Binary AC Bootis. JAAVSO. Vol. 38, 2010.

The objective of the project was to image the eclipsing binary, measure the apparent magnitude, to process the images, and to obtain a light curve. To observe this system, a classmate and I made use of the 20″ Ritchey-Chrétien telescope at the university observatory. We made use of the CCD camera attached and set a sequence of images to be taken every two minutes. W UMa has a period of approximately 8 hours, however, due to time constraints (and as much as I would have liked to, the weather was not conducive for observations exceeding two hours), we ended up only taking images for around two hours.

After the session was over, we ended up taking a total of roughly 40-50 images. Additionally, the software used to capture the images simultaneously measured the magnitude of W UMa at the time each image was taken. This allowed us to use Excel (and later on MATLAB) to obtain a partial light curve. However, since this is a partial light curve, we can say that an eclipse (and a short one at that) occurs, yet we cannot determine whether or not the local minimum depicted in the graph below is a primary or a secondary minimum–we simply do not have enough data.

In addition to the partial light curve above, we were able to process the images (using Registax v.6). Below is a stacked image of W UMa. The big blob near the center of the image is the binary. The binary is not able to be resolved by telescopes component-wise.

References:

Caroll, B.W., and Ostlie, D. A., Introduction to Modern Astrophysics. 2017. Cambridge University Press. 7.

Catalog and Atlas of Eclipsing Binaries (CALEB): Types of Binary Stars

http://www.daviddarling.info/encyclopedia/C/close_binary.html

American Association of Variable Star Observers (AAVSO) URL: https://www.aavso.org/vsots_wuma

Journal of American Association of Variable Star Observers: Figure References

Helicity and Magnetic Helicity

SOURCE FOR CONTENT: Davidson, P.A., 2001, An Introduction to Magnetohydrodynamics. 3.

The purpose of this post is to introduce the concepts of helicity as an integral invariant and its magnetic analog. More specifically, I will be showing that

$\displaystyle h = \int_{V_{\omega}}\textbf{u}\cdot \omega d^{3}r (1)$

is invariant and thus correlates to the conservation of vortex line topology using the approach given in the source material above. I will then discuss magnetic helicity and how it relates to MHD.

Consider the total derivative of $\textbf{u}\cdot \omega$ :

$\displaystyle \frac{D}{Dt}(\textbf{u}\cdot \omega) = \frac{D\textbf{u}}{Dt}\cdot \omega + \frac{D\omega}{Dt}\cdot \textbf{u}, (2)$

where I have used the product rule for derivatives. Also I denote a total derivative as $\frac{D}{Dt} = \frac{\partial}{\partial t}+(\nabla \cdot \textbf{v})$ so as not to confuse it with the notation for an ordinary derivative. Recall the Navier-Stokes’ equation and the vorticity equation

$\displaystyle \frac{\partial \textbf{u}}{\partial t}+(\nabla \cdot \textbf{v})\textbf{u}=\textbf{F}-\frac{1}{\rho}\nabla P + \nu \nabla^{2}\textbf{u}, (3)$

and

$\displaystyle \frac{\partial \omega}{\partial t}+(\nabla \cdot \textbf{v})\omega =(\nabla \cdot \omega)\textbf{u} +\eta \nabla^{2}\omega (4).$

Let $\textbf{F}=0$ and let $\eta \nabla^{2} \omega \equiv 0$ and $\nu \nabla^{2} \textbf{u} \equiv 0$ . Then,

$\displaystyle \frac{D\textbf{u}}{Dt}=-\nabla \frac{P}{\rho}, (5)$

and

$\displaystyle \frac{D\omega}{Dt}=(\nabla \cdot \omega)\textbf{u}. (6)$

If we substitute Eqs. (5) and (6) into Eq.(2), we get

$\displaystyle \frac{D}{Dt}(\textbf{u}\cdot \omega)=-\nabla \frac{P}{\rho}\cdot \omega + (\nabla \cdot \omega)\textbf{u}\cdot \textbf{u}. (7)$

Evaluating each scalar product gives

$\displaystyle -2\nabla \frac{P}{\rho}\omega + \omega u^{2}\nabla = 0. (8)$

If we divide by 2 and note the definition of the scalar product, we may rewrite this as follows

$\displaystyle \nabla \cdot \bigg\{-\frac{P}{\rho}\omega +\frac{u^{2}}{2}\omega\bigg\}=0. (9)$

With this in mind, consider now the total derivative of $(\textbf{u}\cdot \omega)$ multiplied by a volume element $\delta V$ given by

$\displaystyle \frac{D}{Dt}(\textbf{u}\cdot \omega)\delta V = \nabla \cdot \bigg\{-\frac{P}{\rho}\omega +\frac{u^{2}}{2}\omega\bigg\}\delta V. (10)$

When the above equation is integrated over a volume $V_{\omega}$ , the total derivative becomes an ordinary time derivative. Thus, Eq.(10) becomes

$\displaystyle \int_{V_{\omega}}\frac{d}{dt}(\textbf{u}\cdot \omega)dV=\iint_{S_{\omega}}\bigg\{\nabla \cdot [-\frac{P}{\rho}\omega + \frac{u^{2}}{2}\omega ]\bigg\}\cdot d\textbf{S}=0. (11)$

Hence, Eq.(11) shows that helicity is an integral invariant. In this analysis, we have assumed that the fluid is inviscid. If one considers two vortex lines (as Davidson does as a mathematical example), one finds that there exists two contributions to the overall helicity, corresponding to an individual vortex line. If one considers the vorticity multiplied by a volume element, one finds that for each line, their value helicity is the same. Thus, because they are the same, we can say that the overall helicity remains invariant and hence are linked. If they weren’t linked, then the helicity would be 0. In regards to magnetic helicity we define this as

$\displaystyle h_{m}=\int_{V_{B}}\textbf{A}\cdot \textbf{B}dV, (12)$

where $\textbf{A}$ is the magnetic vector potential which is described by the following relations

$\displaystyle \nabla \times \textbf{A}=\textbf{B}, (13.1)$

and

$\displaystyle \nabla \cdot \textbf{A}=0. (13.2)$

Again, we see that magnetic helicity is also conserved. However, this conservation arises by means of Alfven’s theorem of flux freezing in which the magnetic field lines manage to preserve their topology.

“Proof” of Alfven’s Theorem of Flux Freezing

SOURCE FOR CONTENT: Choudhuri, A.R., 2010. Astrophysics for Physicists. Ch. 8.

In the previous post we saw the consequences of different regimes of the magnetic Reynolds’ number under which either diffusion or advection of the magnetic field dominates. In this post, I shall be doing a “proof” of Alven’s Theorem of Flux Freezing. (I hesitate to call it a proof since it lacks the mathematical rigor that one associates with a proof.) Also note in this post, I will be working with the assumption of a high magnetic Reynolds number.

Alfven’s Theorem of Flux Freezing: Suppose we have a surface $S$ located within a plasma at some initial time $t_{0}$ . From the theorem it is known that the flux of the associated magnetic field is linked with surface $S$ by

$\displaystyle \int_{S}\textbf{B}\cdot d\textbf{S}. (1)$

At some later time $t^{\prime}$ , the elements of plasma contained within $S$ at $t_{0}$ move to some other point and will constitute some different surface $M$ . The magnetic flux, linked to $M$ at $t^{\prime}$ by

$\displaystyle \int_{M}\textbf{B}\cdot d\textbf{M}, (2)$

from which we may mathematically state the theorem as

$\displaystyle \int_{S}\textbf{B}\cdot d\textbf{S}=\int_{M}\textbf{B}\cdot d\textbf{M}. (3)$

If we know that the magnetic field evolves in time in accordance to the induction equation we may express Eq.(3) as

$\displaystyle \frac{d}{dt}\int_{S}\textbf{B}\cdot d\textbf{S}=0. (4)$

To confirm that this is true, we note the two ways magnetic flux may change as being due to either (1) some intrinsic variability of the magnetic field strength or (2) movement of the surface. Therefore, either way it follows that

$\displaystyle \frac{d}{dt}\int_{S}\textbf{B}\cdot d\textbf{S}=\int_{S}\frac{\partial \textbf{B}}{\partial t}\cdot d\textbf{S}+\int_{S}\textbf{B}\cdot \frac{d}{dt}(d\textbf{S}). (5)$

Now, consider again the two surfaces. Let us suppose now that $M$ is displaced some distance relative to $S$ . Further, let us also suppose that this displacement occurs during a time interval $t^{\prime}=t_{0}+\delta t.$ Additionally, if we imagine a cylinder formed by projecting a circular cross-section from one surface to the other, we may consider its length to be $\delta l$ with area given by the cross product: $-\delta t \textbf{v}\times \delta\textbf{l}$ . Moreover, since we know that the area of integration is a closed region we see that the integral vanishes (goes to 0). Thus, we may write the difference

$\displaystyle d\textbf{M}-d\textbf{S}-\delta \oint \textbf{v}\times \delta \textbf{l}=0 (6).$

Recall the definition for a derivative, we may apply it to the second term on the right hand side of Eq.(5) to get

$\displaystyle \frac{d}{dt}(d\textbf{S})=\lim_{\delta t\rightarrow 0}\frac{d\textbf{M}-d\textbf{S}}{\delta t}=\oint \textbf{v}\times \delta \textbf{l}. (7)$

Thus the term becomes

$\displaystyle \int_{S}\textbf{B}\cdot \frac{d}{dt}(d\textbf{S})=\int \oint \textbf{B}\cdot (\textbf{v}\times \delta\textbf{l})=\int \oint (\textbf{B}\times \textbf{v})\cdot \delta l. (8)$

Since the integrals that exist interior to the boundary of the surface (call it path $C$ ) vanish and recall Stokes’ theorem

$\displaystyle \oint_{\partial \Omega}\textbf{F}\cdot d\textbf{r}=\int\int_{\Omega} (\nabla \times \textbf{F})\cdot d\Omega,$

and applying it to Eq.(8) we arrive at

$\displaystyle \frac{d}{dt}\int_{S}\textbf{B}\cdot d\textbf{S}=\oint_{\partial S}(\textbf{B}\times\textbf{v}) \cdot \delta \textbf{l}=\int\int_{S}\bigg\{\nabla \times (\textbf{B}\times\textbf{v})\bigg\}\cdot d\textbf{S}. (9)$

Recall that we are dealing with high magnetic Reynolds number, if we use the corresponding form of the induction equation in Eq.(9) we arrive at

$\displaystyle \frac{d}{dt}\int_{S}\textbf{B}\cdot d\textbf{S}=\int\int_{S}d\textbf{S}\cdot \bigg\{ \frac{\partial \textbf{B}}{\partial t}-\nabla\times (\textbf{v}\times \textbf{B})\bigg\}= 0. (10)$

Thus, this completes the “proof”.

Consequences and some Elementary Theorems of the Ideal One-Fluid Magnetohydrodynamic Equations

SOURCE FOR CONTENT:

Priest, E. Magnetohydrodynamics of the Sun, 2014. Cambridge University Press. Ch.2.;

Davidson, P.A., 2001. An Introduction to Magnetohydrodynamics. Ch.4.

We have seen how to derive the induction equation from Maxwell’s equations assuming no charge and assuming that the plasma velocity is non-relativistic. Thus, we have the induction equation as being

$\displaystyle \frac{\partial \textbf{B}}{\partial t}=\nabla \times (\textbf{v}\times \textbf{B})+\lambda \nabla^{2}\textbf{B}. (1)$

Many texts in MHD make the comparison of the induction equation to the vorticity equation

$\displaystyle \frac{\partial \Omega}{\partial t}= \nabla \times (\textbf{v} \times \Omega)+\nu \nabla^{2}\Omega, (2)$

where I have made use of the vector identity

$\nabla \times (\textbf{X}\times \textbf{Y})=\textbf{X}(\nabla \cdot \textbf{Y})-\textbf{Y}(\nabla \cdot \textbf{X})+(\textbf{Y}\cdot \nabla)\textbf{X}-(\textbf{X}\cdot \nabla)\textbf{Y}$ .

Indeed, if we do compare the induction equation (Eq.(1)) to the vorticity equation (Eq.(2)) we easily see the resemblance between the two. The first term on the right hand side of Eq.(1)/ Eq.(2) determines the advection of magnetic field lines/vortex field lines; the second term on the right hand side deals with the diffusion of the magnetic field lines/vortex field lines.

From this, we can impose restrictions and thus look at the consequences of the induction equation (since it governs the evolution of the magnetic field). Furthermore, we see that we can modify the kinematic theorems of classical vortex dynamics to describe the properties of magnetic field lines. After discussing the direct consequences of the induction equation, I will discuss a few theorems of vortex dynamics and then introduce their MHD analogue.

Inherent to this is magnetic Reynold’s number. In geophysical fluid dynamics, the Reynolds number (not the magnetic Reynolds number) is a ratio between the viscous forces per volume and the inertial forces per volume given by

$\displaystyle Re=\frac{ul}{V}, (3)$

where $u, l, V$ represent the typical fluid velocity, length scale and typical volume respectively. The magnetic Reynolds number is the ratio between the advective and diffusive terms of the induction equation. There are two canoncial regimes: (1) $Re_{m}<<1$ , and (2) $Re_{m}>>1$ The former is sometimes called the diffusive limit and the latter is called either the Ideal limit or the infinite conductivity limit (I prefer to call it the ideal limit, since the terms infinite conductivity limit is not quite accurate).

Case I: $Re_{m}<<1$

Consider again the induction equation

$\displaystyle \frac{\partial \textbf{B}}{\partial t}=\nabla \times (\textbf{v}\times \textbf{B})+\lambda\nabla^{2}\textbf{B}.$

If we then assume that we are dealing with incompressible flows (i.e. $(\nabla \cdot \textbf{v})=0$ ) then we can use the aforementioned vector identity to write the induction equation as

$\displaystyle \frac{D\textbf{B}}{Dt}=(\textbf{B}\cdot \nabla)\textbf{v}+\lambda\nabla^{2}\textbf{B}. (4)$

In the regime for which $Re_{m}<<1$ , the induction equation for incompressible flows (Eq.(4)) assumes the form

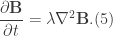
$\displaystyle \frac{\partial \textbf{B}}{\partial t}=\lambda \nabla^{2}\textbf{B}. (5)$

Compare this now to the following equation,

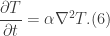
$\displaystyle \frac{\partial T}{\partial t}=\alpha \nabla^{2}T. (6)$

We see that the magnetic field lines are diffused through the plasma.

Case II: $Re_{m}>>1$

If we now consider the case for which the advective term dominates, we see that the induction equation takes the form

$\displaystyle \frac{\partial \textbf{B}}{\partial t}=\nabla \times (\textbf{v}\times \textbf{B}). (7)$

Mathematically, what this suggests is that the magnetic field lines become “frozen-in” the plasma, giving rise to Alfven’s theorem of flux freezing.

Many astrophysical systems require a high magnetic Reynolds number. Such systems include the solar magnetic field (heliospheric current sheet), planetary dynamos (Earth, Jupiter, and Saturn), and galactic magnetic fields.

Kelvin’s Theorem & Helmholtz’s Theorem:

Kelvin’s Theorem: Consider a vortex tube in which we have that $(\nabla \cdot \Omega)=0$ , in which case

$\displaystyle \oint \Omega \cdot d\textbf{S}=0, (8)$

and consider also the curve taken around a closed surface, (we call this curve a material curve $C_{m}(t)$ ) we may define the circulation as being

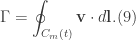
$\displaystyle \Gamma = \oint_{C_{m}(t)}\textbf{v}\cdot d\textbf{l}. (9)$

Thus, Kelvin’s theorem states that if the material curve is closed and it consists of identical fluid particles then the circulation, given by Eq.(9), is temporally invariant.

Helmholtz’s Theorem:

Part I: Suppose we consider a fluid element which lies on a vortex line at some initial time $t=t_{0}$ , according to this theorem it states that this fluid element will continue to lie on that vortex line indefinitely.

Part II: This part says that the flux of vorticity

$\displaystyle \Phi = \int \Omega \cdot d\textbf{S}, (10)$

remains constant for each cross-sectional area and is also invariant with respect to time.

Now the magnetic analogue of Helmholtz’s Theorems are found to be Alfven’s theorem of flux freezing and conservation of magnetic flux, magnetic field lines, and magnetic topology.

The first says that fluid elements which lie along magnetic field lines will continue to do so indefinitely; basically the same for the first Helmholtz theorem.

The second requires a more detailed argument to demonstrate why it works but it says that the magnetic flux through the plasma remains constant. The third says that magnetic field lines, hence the magnetic structure may be stretched and deformed in many ways, but the magnetic topology overall remains the same.

The justification for these last two require some proof-like arguments and I will leave that to another post.

In my project, I considered the case of high magnetic Reynolds number in order to examine the MHD processes present in region of metallic hydrogen present in Jupiter’s interior.

In the next post, I will “prove” the theorems I mention and discuss the project.

Basic Equations of Ideal One-Fluid Magnetohydrodynamics: (Part V) The Energy Equations and Summary

SOURCE FOR CONTENT: Priest E., Magnetohydrodynamics of the Sun, 2014. Ch. 2. Cambridge University Press.

The final subset of equations deals with the energy equations. My undergraduate research did not take into account the thermodynamics of conducting fluid in order to keep the math relatively simple. However, in order to understand MHD one must take into account these considerations. Therefore, there are three essential equations that are indicative of the energy equations:

I. Heat Equation:

We may write this equation in terms of the entropy $S$ as

$\displaystyle \rho T \bigg\{\frac{\partial S}{\partial t}+(\nabla \cdot \textbf{v})S\bigg\}=-\mathcal{L}, (1)$

where $\mathcal{L}$ represents the net effect of energy sinks and sources and is called the energy loss function. For simplicity, one typically writes the form of the heat equation to be

$\displaystyle \frac{\rho^{\gamma}}{\gamma -1}\frac{d}{dt}\bigg\{\frac{P}{\rho^{\gamma}}\bigg\}=-\mathcal{L}. (2)$

2. Conduction

For this equation one considers the explicit form of the energy loss function as being

$\displaystyle \mathcal{L}=\nabla \cdot \textbf{q}+L_{r}-\frac{J^{2}}{\sigma}-F_{H}, (3)$

where $\textbf{q}$ represents heat flux by particle conduction, $L_{r}$ is the net radiation, $J^{2}/\sigma$ is the Ohmic dissipation, and $F_{H}$ represents external heating sources, if any exist. The term $\textbf{q}$ is given by

$\textbf{q}=-\kappa \nabla T, (4)$

where $\kappa$ is the thermal conduction tensor.

3. Radiation

The equation for radiation can be written as a variation of the diffusion equation for temperature

$\displaystyle \frac{DT}{Dt}=\kappa \nabla^{2}T (5)$

where $\kappa$ here denotes the thermal diffusivity given by

$\displaystyle \kappa = \frac{\kappa_{r}}{\rho c_{P}}. (6)$

We may write the final form of the energy equation as

$\displaystyle \frac{\rho^{\gamma}}{\gamma-1}\frac{d}{dt}\bigg\{\frac{P}{\rho^{\gamma}}\bigg\}=-\nabla \cdot \textbf{q}-L_{r}+J^{2}/\sigma+F_{H}, (7)$

where $\textbf{q}$ is given by Eq.(4).

As far as my undergraduate research is concerned, I am including these equations to be complete.

So to summarize the series so far, I have derived most of the basic equations of ideal one-fluid model of magnetohydrodynamics. The equations are

$\displaystyle \frac{\partial \textbf{B}}{\partial t}=(\textbf{v}\times \textbf{B})+\lambda \nabla^{2}\textbf{B}, (A)$

$\displaystyle \frac{\partial \textbf{v}}{\partial t}+(\nabla \cdot \textbf{v})\textbf{v}=-\frac{1}{\rho}\nabla\bigg\{P+\frac{B^{2}}{2\mu_{0}}\bigg\}+\frac{(\nabla \cdot \textbf{B})\textbf{B}}{\mu_{0}\rho}, (B)$

$\displaystyle \frac{\partial \rho}{\partial t}+(\nabla \cdot \rho\textbf{v})=0, (C)$

$\displaystyle \frac{\partial \Omega}{\partial t}+(\nabla \cdot \textbf{v})\Omega = (\nabla \cdot \Omega)\textbf{v}+\nu \nabla^{2}\Omega, (D)$

$\displaystyle P = \frac{k_{B}}{m}\rho T = \frac{\tilde{R}}{\tilde{\mu}}\rho T, (E)$ (Ideal Gas Law)

and

$\displaystyle \frac{\rho^{\gamma}}{\gamma-1}\frac{d}{dt}\bigg\{\frac{P}{\rho^{\gamma}}\bigg\}=-\nabla \cdot \textbf{q}-L_{r}+J^{2}/\sigma +F_{H}. (F)$

We also have the following ancillary equations

$\displaystyle (\nabla \cdot \textbf{B})=0, (G.1)$

since we haven’t found evidence of the existence of magnetic monopoles. We also have that

$\displaystyle \nabla \times \textbf{B}=\mu_{0}\textbf{J}, (G.2)$

where we are assuming that the plasma velocity $v << c$ (i.e. non-relativistic). Finally for incompressible flows we know that $(\nabla \cdot \textbf{v})=0$ corresponding to isopycnal flows.

In the next post, I will discuss some of the consequences of these equations and some elementary theorems involving conservation of magnetic flux and magnetic field line topology.

Monte Carlo Simulations of Radiative Transfer: Basics of Radiative Transfer Theory (Part IIa)

SOURCES FOR CONTENT:

Chandrasekhar, S., 1960. “Radiative Transfer”. Dover. 1.
Choudhuri, A.R., 2010. “Astrophysics for Physicists”. Cambridge University Press. 2.
Boyce, W.E., and DiPrima, R.C., 2005. “Elementary Differential Equations”. John Wiley & Sons. 2.1.

Recall from last time , the radiative transfer equation

$\displaystyle \frac{1}{\epsilon \rho}\frac{dI_{\nu}}{ds}= M_{\nu}-N_{\nu}I_{\nu}, (1)$

where $M_{\nu}$ and $N_{\nu}$ are the emission and absorption coefficients, respectively. We can further define the absorption coefficient to be equivalent to $\epsilon \rho$ . Hence,

$\displaystyle N_{\nu}=\frac{d\tau_{\nu}}{ds}, (2)$

which upon rearrangement and substitution in Eq. (1) gives

$\displaystyle \frac{dI_{\nu}(\tau_{\nu})}{d\tau_{\nu}}+I_{\nu}(\tau_{\nu})= U_{\nu}(\tau_{\nu}). (3)$

We may solve this equation by using the method of integrating factors, by which we multiply Eq.(3) by some unknown function (the integrating factor) $\mu(\tau_{\nu})$ yielding

$\displaystyle \mu(\tau_{\nu})\frac{dI_{\nu}(\tau_{\nu})}{d\tau_{\nu}}+\mu(\tau_{\nu})I_{\nu}(\tau_{\nu})=\mu(\tau_{\nu})U_{\nu}(\tau_{\nu}). (4)$

Upon examining Eq.(4), we see that the left hand side is the product rule. It follows that

$\displaystyle \frac{d}{d\tau_{\nu}}\bigg\{\mu(\tau_{\nu})I_{\nu}(\tau_{\nu})\bigg\}=\mu({\tau_{\nu}})U_{\nu}(\tau_{\nu}). (5)$

This only works if $d(\mu(\tau_{\nu}))/d\tau_{\nu}=\mu(\tau_{\nu})$ . To show that this is valid, consider the equation for $\mu(\tau_{\nu})$ only:

$\displaystyle \frac{d\mu(\tau_{\nu})}{d\tau_{\nu}}=\mu(\tau_{\nu}). (6.1)$

This is a separable ordinary differential equation so we can rearrange and integrate to get

$\displaystyle \int \frac{d\mu(\tau_{\nu})}{\mu(\tau_{\nu})}=\int d\tau_{\nu}\implies \ln(\mu(\tau_{\nu}))= \tau_{\nu}+C, (6.2)$

where $C$ is some constant of integration. Let us assume that the constant of integration is $0$ , and let us also take the exponential of (6.2). This gives us

$\displaystyle \mu(\tau_{\nu})=\exp{(\tau_{\nu})}. (6.3)$

This is our integrating factor. Just as a check, let us take the derivative of our integrating factor with respect to $d\tau_{\nu}$ ,

$\displaystyle \frac{d}{d\tau_{\nu}}\exp{(\tau_{\nu})}=\exp{(\tau_{\nu})},$

Thus this requirement is satisfied. If we now return to Eq.(4) and substitute in our integrating factor we get

$\displaystyle \frac{d}{d\tau_{\nu}}\bigg\{\exp{(\tau_{\nu})}I_{\nu}(\tau_{\nu})\bigg\}=\exp{(\tau_{\nu})}U_{\nu}(\tau_{\nu}). (7)$

We can treat this as a separable differential equation so we can integrate immediately. However, we are integrating from an optical depth $0$ to some optical depth $\tau_{\nu}$ , hence we have that

$\displaystyle \int_{0}^{\tau_{\nu}}d\bigg\{\exp{(\tau_{\nu})}I_{\nu}(\tau_{\nu})\bigg\}=\int_{0}^{\tau_{\nu}}\bigg\{\exp{(\bar{\tau}_{\nu})}U_{\nu}(\bar{\tau}_{\nu})\bigg\}d\bar{\tau}_{\nu}, (8)$

We find that

$\displaystyle \exp{(\tau_{\nu})}I_{\nu}(\tau_{\nu})-I_{\nu}(0)=\int_{0}^{\tau_{\nu}}\bigg\{\exp{(\bar{\tau}_{\nu})}U_{\nu}(\bar{\tau}_{\nu})\bigg\}d\bar{\tau}_{\nu} (9),$

where if we add $I_{\nu}(0)$ and divide by $\exp{(\tau_{\nu})}$ we arrive at the general solution of the radiative transfer equation

$\displaystyle I_{\nu}(\tau_{\nu}) = I_{\nu}(0)\exp{(-\tau_{\nu})}+\int_{0}^{\tau_{\nu}}\exp{(\bar{\tau}_{\nu}-\tau_{\nu})}U_{\nu}(\bar{\tau}_{\nu})d\bar{\tau}_{\nu}. (10)$

This is the mathematically formal solution to the radiative transfer equation. While mathematically sound, much of the more interesting physical phenomena require more complicated equations and therefore more sophisticated methods of solving them (an example would be the use of quadrature formulae or $n$ -th approximation for isotropic scattering).

Recall also that in general we can write the phase function $p(\theta,\phi; \theta^{\prime},\phi^{\prime})$ via the following

$\displaystyle p(\theta,\phi;\theta^{\prime},\phi^{\prime})=\sum_{l=0}^{\infty}\gamma_{l}P_{l}(\cos{\Theta}). (11)$

Let us consider the case for which $l=0$ in the sum given by (11). This then would mean that the phase function is constant

$p(\theta,\phi;\theta^{\prime},\phi^{\prime})=\gamma_{0}=const. (12)$

Such a phase function is consistent with isotropic scattering. The term isotropic means, in this context, that radiation scattered is the same in all directions. Such a case yields a source function of the form

$\displaystyle U_{\nu}(\tau_{\nu})=\frac{1}{4\pi}\int_{0}^{\pi}\int_{0}^{2\pi}\gamma_{0}I_{\nu}(\tau_{\nu})\sin{\theta^{\prime}}d\theta^{\prime}d\phi^{\prime}, (13)$

where upon use in the radiative transfer equation we get the integro-differential equation

$\displaystyle \frac{dI_{\nu}(\tau_{\nu})}{d\tau_{\nu}}+I_{\nu}(\tau_{\nu})= \frac{1}{4\pi}\int_{0}^{\pi}\int_{0}^{2\pi}\gamma_{0}I_{\nu}(\tau_{\nu})\sin{\theta^{\prime}}d\theta^{\prime}d\phi^{\prime}. (14)$

Solution of this equation is beyond the scope of the project. In the next post I will discuss Rayleigh scattering and the corresponding phase function.

Monte Carlo Simulations of Radiative Transfer: Basics of Radiative Transfer Theory (Part I)

SOURCE FOR CONTENT: Chandrasekhar, S., 1960. Radiative Transfer. 1.

In this post, I will be discussing the basics of radiative transfer theory necessary to understand the methods used in this project. I will start with some definitions, then I will look at the radiative transfer equation and consider two simple cases of scattering.

The first definition we require is the specific intensity, which is the amount of energy associated with a specific frequency $dE_{\nu}$ passing through an area $dA$ constrained to a solid angle $d\Omega$ in a time $dt$ . We may write this mathematically as

$dE_{\nu}=I_{\nu}\cos{\theta}d\nu d\Sigma d\Omega dt. (1)$

We must also consider the net flux given by

$\displaystyle d\nu d\Sigma dt \int I_{\nu}\cos{\theta}d\Omega, (2)$

where if we integrate over all solid angles $\Omega$ we get

$\pi F_{\nu}=\displaystyle \int I_{\nu}\cos{\theta}d\Omega. (3)$

Let $d\Lambda$ be an element of the surface $\Lambda$ in a volume $V$ through which radiation passes. Further let $\Theta$ and $\theta$ denote the angles which form normals with respect to elements $d\Lambda$ and $d\Sigma$ . These surfaces are joined by these normals and hence we have the surface across which energy flows includes the elements $d\Lambda$ and $d\Sigma$ , given by the following:

$I_{\nu}\cos{\Theta}d\Sigma d\Omega^{\prime}d\nu = I_{\nu}d\nu \frac{\cos{\Theta}\cos{\theta}d\Sigma d\Lambda}{r^{2}} (4),$

where $d\Omega^{\prime}=d\Lambda \cos{\Theta}/r^{2}$ is the solid angle subtended by the surface element $d\Lambda$ at a point $P$ and volume element $dV=ld\Sigma \cos{\theta}$ is the volume that is intercepted in volume $V$ . If we take this further, and integrate over all $V$ and $\Omega$ we arrive at

$\displaystyle \frac{d\nu}{c}\int dV \int I_{\nu} d\Omega=\frac{V}{c}d\nu \int I_{\nu}d\Omega, (5)$

where if the radiation travels some distance $L$ in the volume, then we must multiply Eq.(5) by $l/c$ , where $c$ is the speed of light.

We now define the integrated energy density as being

$U_{\nu}=\displaystyle \frac{1}{c}\int I_{\nu}d\Omega, (6.1)$

while the average intensity is

$J_{\nu}=\displaystyle \frac{1}{4\pi}\int I_{\nu}d\nu, (6.2)$

and the relation between these two equations is

$U_{\nu}=\frac{4\pi}{c}J_{\nu}. (6.3)$

I will now introduce the radiative transfer equation. This equation is a balance between the amount of radiation absorbed and the radiation that is emitted. The equation is,

$\frac{dI_{\nu}}{ds}=-\epsilon \rho I_{\nu}+h_{\nu}\rho, (7)$

where if we divide by $\epsilon \rho$ we get

$-\frac{1}{\epsilon_{\nu}\rho}\frac{dI_{\nu}}{ds}=I_{\nu}+U_{\nu}(\theta, \phi), (8)$

where $U(\theta,\phi)$ represents the source function given by

$U_{\nu}(\theta,\phi)=\displaystyle \frac{1}{4\pi}\int_{0}^{\pi}\int_{0}^{2\pi}p(\theta,\phi;\theta^{\prime},\phi^{\prime})I_{\nu}\sin{\theta^{\prime}}d\theta^{\prime}d\phi^{\prime}. (9)$

The source function is typically the ratio between the absorption and emission coefficients. One of the terms in the source function is the phase function which varies according to the specific scattering geometry. In its most general form, we can represent the phase function as an expansion of Legendre polynomials:

$p(\theta, \phi; \theta^{\prime},\phi^{\prime})=\displaystyle \sum_{j=0}^{\infty}\gamma_{j}P_{j}(\mu), (10)$

where we have let $\mu = \cos{\theta}$ (in keeping with our notation in previous posts).

In Part II, we will discuss a few simple cases of scattering and their corresponding phase functions, as well as obtaining the formal solution of the radiative transfer equation. (DISCLAIMER: While this solution will be consistent in a mathematical sense, it is not exactly an insightful solution since much of the more interesting and complex cases involve the solution of either integro-differential equations or pure integral equations (a possible new topic).)

Monte Carlo Simulations of Radiative Transfer: Project Overview

The goal of this project was to simulate radiative transfer in the circumbinary disk GG Tau by using statistical methods (i.e. Monte Carlo methods). To provide some context for the project, I will describe the astrophysical system that I considered, and I will describe the objectives of the project

Of the many stars in the night sky, a significant number of them, when you are able to resolve them, are in fact binary stars. These are star systems in which two stars orbit a common center of mass known as a barycenter. For this reason, we regard GG Tau to be a close binary system; a system in which two stars are separated by a significant distance comparable to the diameters of each star.

The system of GG Tau has four known components with a hypothesized fifth component. There is a disk of material encircling the entire system which we call a circumbinary disk. Additionally, there is also an inner disk of material that surrounds the primary and secondary components referred to as a circumstellar disk.

The goal of this project was to use Monte Carlo methods to simulate radiative transfer processes present in GG Tau. This is accomplished through the use of importance sampling two essential quantities over cumulative distribution function of the form

$\displaystyle \xi=\int_{0}^{L} \mathcal{P}(x)dx\equiv \psi(x_{0}), (1)$

using FORTRAN code. I will discuss the mathematical background of probability and Monte Carlo methods (stochastic processes) in more detail in a later post. The general process of radiative transfer is relatively simple. Starting with an emitter, radiation travels from its emission point, travels a certain distance, and at this point the radiation could either be scattered into an angle different from the incidence angle, or it can be absorbed by the material. In the context of this project, the emitter (or emitters) are the primary and secondary components of GG Tau. The radiation emitted is electromagnetic radiation, or light. This light will travel a distance $L$ after which the light is either scattered or absorbed. The code uses Eq.(1) (cumulative distribution function) to sample optical depths and scattering angles to calculate the distance traveled $L$ . I will reserve the exact algorithm for a future post as well. In the next post, I will discuss the basics of radiative transfer theory as presented in the text “Radiative Transfer” by S. Chandrasekhar, 1960.

The following are the sources used in this project

Wood, K., Whitney, B., Bjorkman, J., and Wolff M., 2013. Introduction to Monte Carlo Radiative Transfer.

Whitney, B. A., 2011. Monte Carlo Radiative Transfer. Bull. Astr. Soc. India.

Kitamura, Y., Kawabe, R., Omodaka, T., Ishiguro, M., and Miyama, S., 1994. Rotating Protoplanetary Gas Disk in GG Tau. ASP Conference Series. Vol. 59.

Piètu, V., Gueth, F., Hily-Blant, P., Schuster, K.F., and Pety, J., 2011. High Resolution Imaging of the GG Tauri system at 267 GHz. Astronomy & Astrophysics. 528. A81.

Skrutskie, M.F., Snell, R.L., Strom, K.M., Strom, S.E., and Edwards, S., 1993. Detection of Circumstellar Gas Associated with GG Tauri. The Astrophysical Journal. 409:422-428.

Choudhuri, A.R., 2010. Astrophysics for Physicists. 2.

Carroll B.W., Ostlie, D.A., 2007. An Introduction to Modern Astrophysics. 9,10.

Chandrasekhar, S., 1960. Radiative Transfer. 1.

Schroeder, D., 2000. Introduction to Thermal Physics. 8.

Ross, S., 2010. Introduction to Probability Model. 2,4,11.

I obtained the FORTRAN code from K. Wood via the following link. (For the sake of completeness the URL is: www-star.st-and.ac.uk/~kw25/research/montecarlo/montecarlo.html)

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this: