Month: May 2018

Coordinates and Transformations of Coordinates

SOURCES FOR CONTENT:  Neuenschwander, D.E., Tensor Calculus for Physics, 2015. Johns Hopkins University Press. 

In this post, I continue the introduction of tensor calculus by discussing coordinates and coordinate transformations as applied to relativity theory. (A side note: I have acquired Misner, Thorne, and Wheeler’s Gravitation and will be using it sparingly given its reputation and weight of the material.)

Continue reading Coordinates and Transformations of Coordinates

Derivation of the Finite-Difference Equations

In my final semester, my course load included a graduate course that had two modules: astronomical instrumentation and numerical modeling. The latter focused on developing the equations of motion of geophysical fluid dynamics (See Research in Magnetohydrodynamics). Such equations are then converted into an algorithm based on a specific type of numerical method of solving the exact differential equation.

The purpose of this post is to derive the finite-difference equations. Specifically, I will be deriving the forward, backward, centered first order equations. We start with the Taylor expansion about the points x_{0}= \pm h:

\displaystyle f(x+h)=\sum_{n=1}^{\infty}\frac{h^{n}}{n!}\frac{d^{n}f}{dx^{n}}, (1)

and

\displaystyle f(x-h)=\sum_{n=1}^{\infty}(-1)^{n}\frac{h^{n}}{n!}\frac{d^{n}f}{dx^{n}}. (2)

Let f(x_{j})=f_{j}, f(x_{j}+h)=f_{j+1}, f(x_{j}-h)=f_{j-1}. Therefore, if we consider the following differences…

\displaystyle f_{j+1}-f_{j}=f^{\prime}_{j}+f^{\prime \prime}_{j}\frac{h^{2}}{2!}+...+f^{n}_{j}\frac{h^{n}}{n!}, (3)

and

\displaystyle f_{j}-f_{j-1}=hf^{\prime}_{j}-\frac{h^{2}}{2!}f^{\prime \prime}_{j}+...\mp \frac{h^{n}}{n!}f^{n}_{j}, (4)

and

\displaystyle f_{j+1}-f_{j-1}=2hf^{\prime}_{j}+\frac{2h^{3}}{3!}f^{\prime\prime\prime}_{j}+..\mp \frac{h^{n}}{n!}f^{n}_{j}, (5)

and if we keep only linear terms, we get

\displaystyle f^{\prime}_{j}=\frac{f_{j+1}-f_{j}}{h}+\mathcal{O}(h), (6)

\displaystyle f^{\prime}_{j}=\frac{f_{j}-f_{j-1}}{h}+\mathcal{O}(h), (7)

and

\displaystyle f^{\prime}_{j}=\frac{f_{j+1}-f_{j-1}}{2h}+\mathcal{O}(h)

where the first is the forward difference, the second is the backward difference, the last is the centered difference, and \mathcal{O}(h) represents the quadratic, cubic, quartic,quintic,etc. terms. One can use similar logic to derive the second-order finite-difference equations.

 

Helicity and Magnetic Helicity

SOURCE FOR CONTENT: Davidson, P.A., 2001, An Introduction to Magnetohydrodynamics. 3. 

The purpose of this post is to introduce the concepts of helicity as an integral invariant and its magnetic analog. More specifically, I will be showing that

\displaystyle h = \int_{V_{\omega}}\textbf{u}\cdot \omega d^{3}r  (1)

is invariant and thus correlates to the conservation of vortex line topology using the approach given in the source material above.  I will then discuss magnetic helicity and how it relates to MHD.

Consider the total derivative of \textbf{u}\cdot \omega:

\displaystyle \frac{D}{Dt}(\textbf{u}\cdot \omega) = \frac{D\textbf{u}}{Dt}\cdot \omega + \frac{D\omega}{Dt}\cdot \textbf{u}, (2)

where I have used the product rule for derivatives. Also I denote a total derivative as \frac{D}{Dt} = \frac{\partial}{\partial t}+(\nabla \cdot \textbf{v}) so as not to confuse it with the notation for an ordinary derivative. Recall the Navier-Stokes’ equation and the vorticity equation

\displaystyle \frac{\partial \textbf{u}}{\partial t}+(\nabla \cdot \textbf{v})\textbf{u}=\textbf{F}-\frac{1}{\rho}\nabla P + \nu \nabla^{2}\textbf{u}, (3)

and

\displaystyle \frac{\partial \omega}{\partial t}+(\nabla \cdot \textbf{v})\omega =(\nabla \cdot \omega)\textbf{u} +\eta \nabla^{2}\omega (4).

Let \textbf{F}=0 and let \eta \nabla^{2} \omega \equiv 0 and \nu \nabla^{2} \textbf{u} \equiv 0. Then,

\displaystyle \frac{D\textbf{u}}{Dt}=-\nabla \frac{P}{\rho},  (5)

and

\displaystyle \frac{D\omega}{Dt}=(\nabla \cdot \omega)\textbf{u}. (6)

If we substitute Eqs. (5) and (6) into Eq.(2), we get

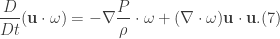
\displaystyle \frac{D}{Dt}(\textbf{u}\cdot \omega)=-\nabla \frac{P}{\rho}\cdot \omega + (\nabla \cdot \omega)\textbf{u}\cdot \textbf{u}. (7)

Evaluating each scalar product gives

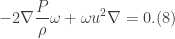
\displaystyle -2\nabla \frac{P}{\rho}\omega + \omega u^{2}\nabla = 0. (8)

If we divide by 2 and note the definition of the scalar product, we may rewrite this as follows

\displaystyle \nabla \cdot \bigg\{-\frac{P}{\rho}\omega +\frac{u^{2}}{2}\omega\bigg\}=0. (9)

With this in mind, consider now the total derivative of 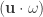(\textbf{u}\cdot \omega) multiplied by a volume element \delta V given by

\displaystyle \frac{D}{Dt}(\textbf{u}\cdot \omega)\delta V = \nabla \cdot \bigg\{-\frac{P}{\rho}\omega +\frac{u^{2}}{2}\omega\bigg\}\delta V. (10)

When the above equation is integrated over a volume V_{\omega}, the total derivative becomes an ordinary time derivative. Thus, Eq.(10) becomes

\displaystyle \int_{V_{\omega}}\frac{d}{dt}(\textbf{u}\cdot \omega)dV=\iint_{S_{\omega}}\bigg\{\nabla \cdot [-\frac{P}{\rho}\omega + \frac{u^{2}}{2}\omega ]\bigg\}\cdot d\textbf{S}=0. (11)

Hence, Eq.(11) shows that helicity is an integral invariant. In this analysis, we have assumed that the fluid is inviscid. If one considers two vortex lines (as Davidson does as a mathematical example), one finds that there exists two contributions to the overall helicity, corresponding to an individual vortex line. If one considers the vorticity multiplied by a volume element, one finds that for each line, their value helicity is the same. Thus, because they are the same, we can say that the overall helicity remains invariant and hence are linked. If they weren’t linked, then the helicity would be 0. In regards to magnetic helicity we define this as

\displaystyle h_{m}=\int_{V_{B}}\textbf{A}\cdot \textbf{B}dV, (12)

where \textbf{A} is the magnetic vector potential which is described by the following relations

\displaystyle \nabla \times \textbf{A}=\textbf{B}, (13.1)

and

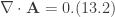
\displaystyle \nabla \cdot \textbf{A}=0. (13.2)

 Again, we see that magnetic helicity is also conserved. However, this conservation arises by means of Alfven’s theorem of flux freezing in which the magnetic field lines manage to preserve their topology.